COME CALCOLARE GLI ANGOLI INTERNI ESTERNI DI UN POLIGONO

COME CALCOLARE GLI ANGOLI INTERNI ESTERNI DI UN POLIGONO

Sappiamo quanto semplice sia trovare l'ampiezza degli angoli interni di un triangolo equilatero oppure di uno isoscele ma la procedura per il calcolo dell'ampiezza degli angoli di un poligono è diversa (parliamo di un poligono regolare). Questo perchè un poligono può avere diverso numero di lati, pensiamo al pentagramma o all'ottagono. Oggi vediamo quindi la formula per calcolare gli angoli interni ed esterni di un poligono, di una figura data. Come fare a trovare la formula finale per trovare ampiezza dei lati interni ed esterni ? Bene, diciamo che la formula è davvero molto semplice ed anche come ci si arriva.

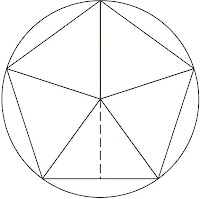
Partiamo dagli angoli interni. Abbiamo un poligono che presenta un centro. Uniamo questo centro ai diversi vertici. Se possediamo un pentagono avremo 5 vertici e si formeranno così 5 triangoli interni che sono 5 triangoli isosceli. Ogni triangolo sappiamo che ha la somma interna degli angoli di 180 gradi. Chiamiamo Nt il numero dei triangoli che si formano all'interno dopo l'unione del centro del poligono con i vertici.

Se ogni triangolo è composto da 180 come somma degli angoli interni allora 180 x Nt (numero triangoli) ci darà la somma totale di tutti gli angoli interni ma attenzione perchè in questa somma stiamo calcolando anche i 5 angoli che si formano al centro del poligono. Dobbiamo quindi eliminare questi angoli dalla formula. Lo facciamo davvero molto semplicemente perchè i 5 angoli al centro della figura formano esattamente 360 gradi. Quindi dalla formula 180 x Nt basta sottrarre 360 ed otterremo la somma degli angoli interni di una figura. Ecco la formula :

Somma angoli interni = (180 x Nt) - 360

che possiamo semplificare dato che 360 può essere visto come 180 x 2 e quindi :

Somma angoli interni = 180 x (Nt-2)

Ovviamente un singolo angolo sarà dato dalla formula :

Angolo interno = [180 x (Nt-2)] / Nt

Come faccio a calcolare gli angoli esterni del poligono a questo punto ? Facile anche questo visto che ogni angolo esterno è complementare al suo interno e quindi se abbiamo trovato che un angolo interno è pari a 60 gradi, quello esterno sarà pari a 180 meno 60. In generale, visto che gli angoli interni di un poligono quale l'esagono, il quadrato, il rettangolo, il pentagono, ecc..., sono uguali, allora la formula per calcolare ogni angolo esterno è :

Somma angoli esterni = 360 / Nt

Semplicissimo. Vediamo un esempio e poi potrete fare degli esercizi. Abbiamo un pentagono regolare che possiede 5 lati (Nt = 5). Calcolate il valore di ciascun angolo interno ed esterno.

Angolo interno = [180 x (Nt-2)] / Nt = (180 x 3) / 5 = 108 gradi

Angolo esterno = 360 / Nt = 360 / 5 = 72 gradi

Il pentagono ha quindi ciascuno dei 5 angoli interni pari a 108 gradi e ciascuno degli esterni pari a 72 gradi. Infatti la somma di un angolo interno con quello esterno fa 108 + 72 = 180 gradi (angoli complementari).

ESERCIZI SUL CALCOLO DEGLI ANGOLI INTERNI ED ESTERNI

1. Calcolare la misura dell'ampiezza di un angolo esterno di un esagono regolare.
2. Calcolare la misura dell'ampiezza di un angolo interno di un ottagono regolare.
3. Calcolare la misura dell'ampiezza di un angolo interno ed esterno di un dodecagono regolare.

Se cercate problemi sulla geometria e su diverse figure geometriche, esercizi di matematica su espressioni, frazioni, integrali ed esercizi sulla grammatica italiana e straniera, allora vi consiglio di visitare questa pagina web :

TUTTO SU GEOMETRIA MATEMATICA GRAMMATICA

Iscriviti al mio FEED RSS